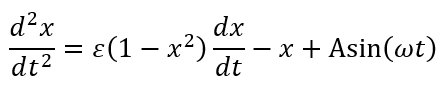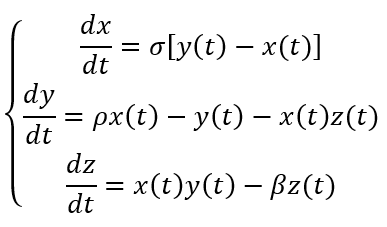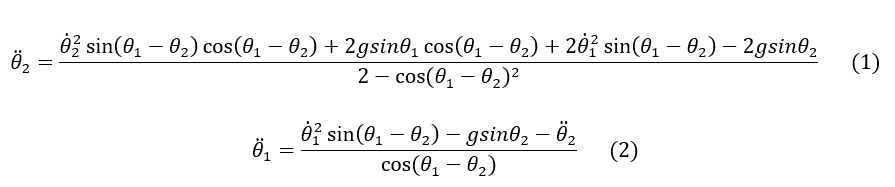Le chaos pour les curieux !
Le chaos, une introduction
Le chaos désigne le comportement de systèmes physiques particuliers dont l’évolution temporelle présente une forte dépendance aux conditions initiales : des conditions initiales proches amènent à des évolutions significativement différentes. Dans le cas du chaos déterministe, ces systèmes sont parfaitement modélisables.
Un des exemples les plus simples de mouvement chaotique est le double pendule, constitué de deux segments rigides reliés par une articulation, le tout oscillant dans un plan vertical. Le segment supérieur est attaché à un support articulé, le segment inférieur est libre et suit le premier dans son mouvement.
Ce système est facile à mettre en place et à étudier en laboratoire : on constate qu’une petite différence dans les positions spatiales initiales des segments au moment du lâcher amène ultérieurement à une variation importante des positions.
La modélisation de ce système ne présente pas non plus de difficulté, ce qui permet de l’étudier par simulation informatique.
Un exemple un peu plus compliqué à mettre en œuvre, mais toujours accessible à l’expérimentation en laboratoire, est l’oscillateur de Van der Pol. Il s’agit d’un circuit électronique qui présente un comportement chaotique sous certaines conditions. On peut relativement facilement modéliser la tension électrique présentant le caractère chaotique.
Un exemple beaucoup plus complexe est l’évolution de la situation météorologique. Le système atmosphérique est impossible à reproduire en laboratoire. C’est l’observation et l’étude de la succession des différents types de temps en un endroit donné sur une période plus ou moins longue qui permet de conclure à l’aspect chaotique du temps qu’il fait dans la troposphère.
Une modélisation approchée et particulièrement complexe du système atmosphérique est possible et permet les prévisions du temps. Ces modèles et les simulations du temps démontrent la grande sensibilité du système aux conditions initiales.
Dans ce qui suit nous allons présenter successivement quatre exemples de systèmes chaotiques qui seront modélisés en utilisant un outil de simulation aisé à manipuler : le langage de programmation Python. Les codes pour obtenir ces diverses animations et graphiques sont également mis à disposition.
Ces systèmes sont :
1). La suite logistique, qui est un modèle mathématique simple de situations chaotiques, mais avec des résultats assez spectaculaires ;
2). L’oscillateur de Van der Pol, qui amène à résoudre une équation différentielle à une variable ;
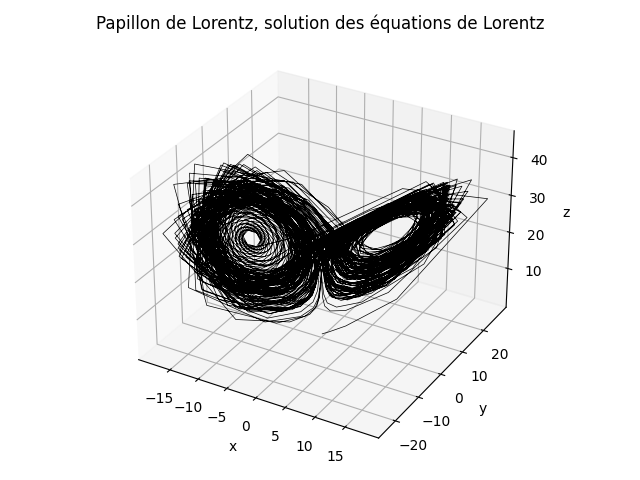
3). Les équations différentielles de Lorenz (le météorologue, vers 1960), représentant une simulation très simplifiée du système atmosphérique. Ces équations permettent de dessiner le fameux papillon de Lorentz !
4). Le pendule double, système de deux équations différentielles à deux variables, couplées ;
1). La suite logistique
La suite est décrite par la relation de récurrence non linéaire suivante :
Cette suite peut décrire une population d’individus (des loups par exemple…), xt étant le rapport entre la population à l’instant t et la population maximale ; xt+1 est le même rapport, à un instant t + Δt.
k est un paramètre, un nombre réel positif.
Il est facile de démontrer que cette définition implique que xt ∈ [0 , 1] . Cela a pour conséquence que k ∈ [0 ,4].
Le premier terme du membre de droite kxt aura comme influence d’augmenter la population, le deuxième terme –kxt² aura tendance à la diminuer. La population va évoluer selon la compétition entre ces deux termes et pour certaines valeurs de k, l’évolution sera chaotique.
Pour calculer les termes de cette suite, on commence par choisir une valeur initiale x0, généralement égale à ½. Cette première valeur correspond au paramètre t = 0. On insère cette valeur dans le membre de droite et l’on trouve un résultat qui nous donne le deuxième terme de la suite (le terme t+1) , soit x1, correspondant au paramètre t = 1. Et on recommence en insérant ce nouveau terme dans le membre de droite pour obtenir x2, etc.
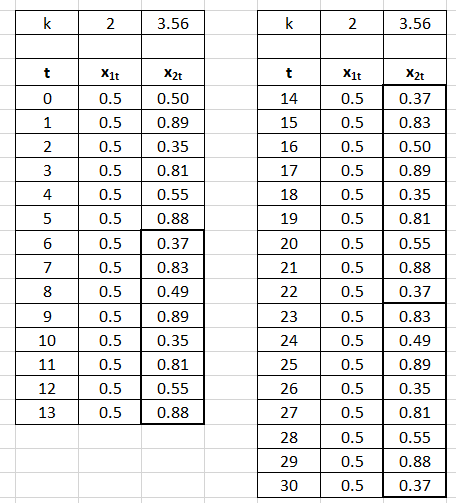
On peut faire ces calculs très simples avec excel par exemple. Dans la table ci-dessous, on montre un exemple pour les 30 premiers termes de deux suites : la première x1t, avec k = 2 et x0 = 0.5 ; et la seconde, x2t, avec k = 3.56 et x0 = 0.5.
La première suite converge immédiatement vers 0.5, la seconde oscille périodiquement autour de 8 valeurs, appelés les points d’accumulation, que l’on voit apparaître entre t=6 et t=13, puis t=14 et t=21, etc. Ces séries de points sont encadrées en gras dans le tableau. Les résultats ont été arrondis au 1/100 ème. t est le paramètre d’itération utilisé pour définir la suite.
Les figures 1 et 2 montrent deux résultats de calculs réalisés avec Python.
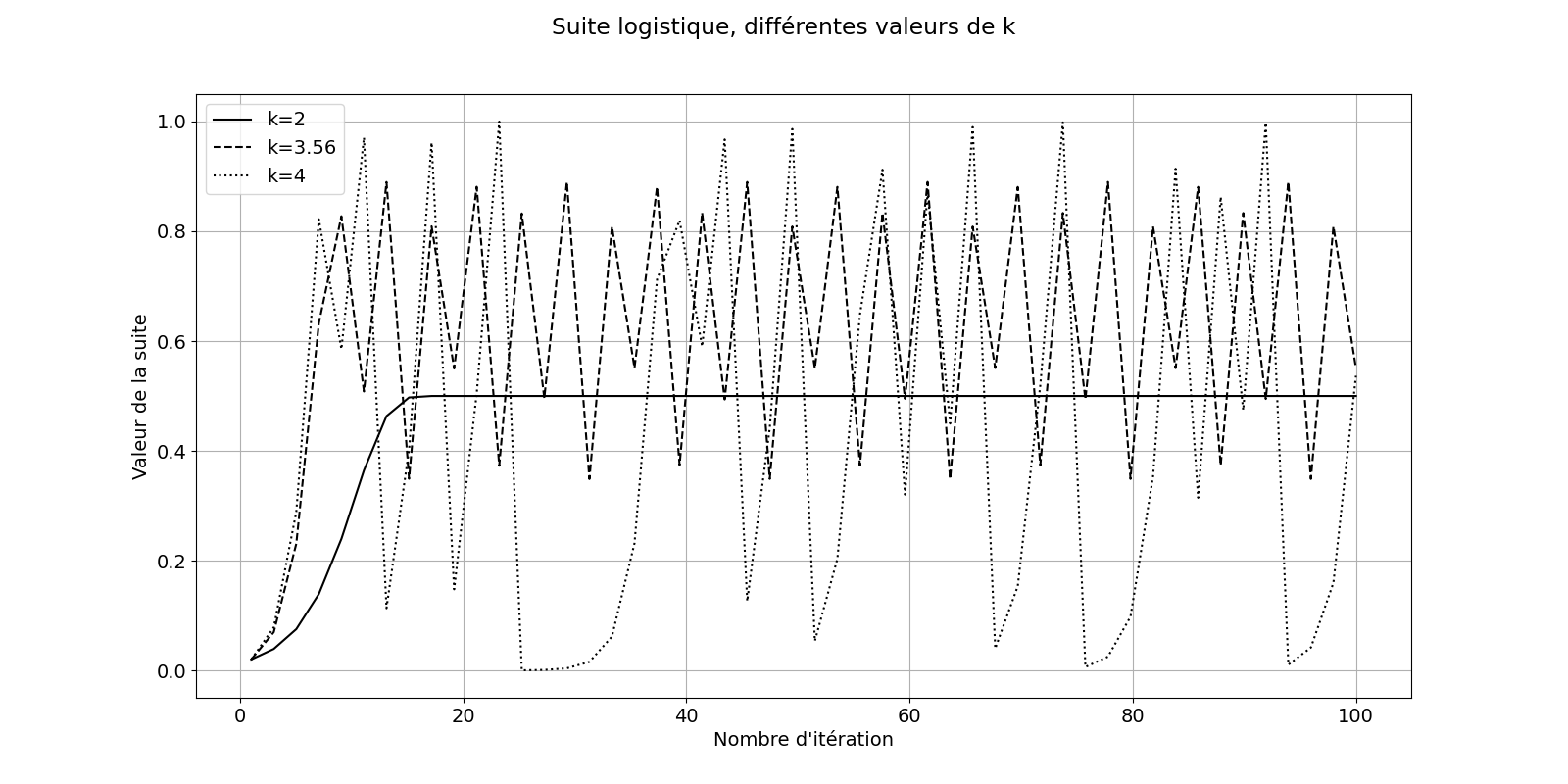
Figure 1. Evolution de x en fonction du nombre d’itérations, pour une même valeur initiale x0 et pour trois valeurs de k différentes. Pour k = 2, la population augmente et se stabilise assez rapidement vers x = 0.5. Pour k = 3.56, la population oscille périodiquement autour de huit valeurs de x. Cela signifie que ces huit valeurs de la population se succèdent. Ces valeurs sont appelées « points d’accumulation ». Enfin pour k = 4, on a un comportement chaotique : sur le nombre d’itérations représenté, aucune structure périodique ne peut être décelée. Code Python pour réaliser cette figure: chaos fig 1
Cliquer sur l’image pour l’agrandir
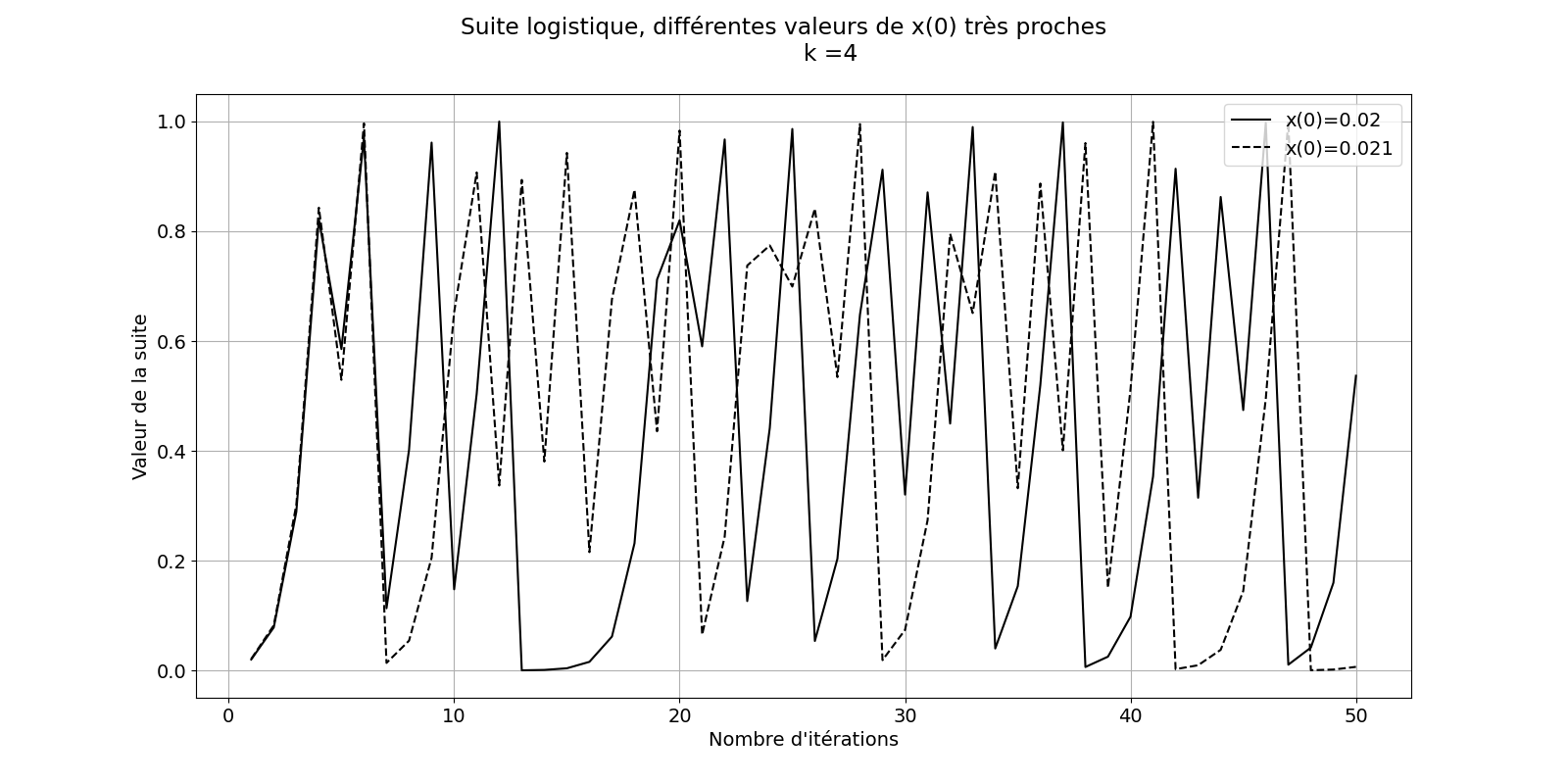
Figure 2. Représentation de la valeur de x en fonction du nombre d’itérations, pour k = 4 et deux valeurs initiales x0 très proches, soit x0 = 0.02 et x0 = 0.021. On voit qu’au départ, les valeurs sont assez proches jusqu’à la 7ème itération. Ensuite les valeurs obtenues divergent assez clairement tout en montrant une absence de périodicité. On a là un exemple de sensibilité aux conditions initiales. Code Python pour réaliser cette figure: chaos fig 2
Cliquer sur l’image pour l’agrandir
Une autre façon de considérer et d’étudier la suite est son diagramme de bifurcation, qui représente les valeurs de la suite en fonction de la valeur du paramètre k, soit les points (k, ut). Ce diagramme fait ressortir les points d’accumulation de la suite, c’est-à-dire les valeurs limites atteintes par les termes de la suite, entre le 100ème et le 199ème terme. Le nombre de ces valeurs limites ou points d’accumulation, varient suivant la valeur du paramètre k.
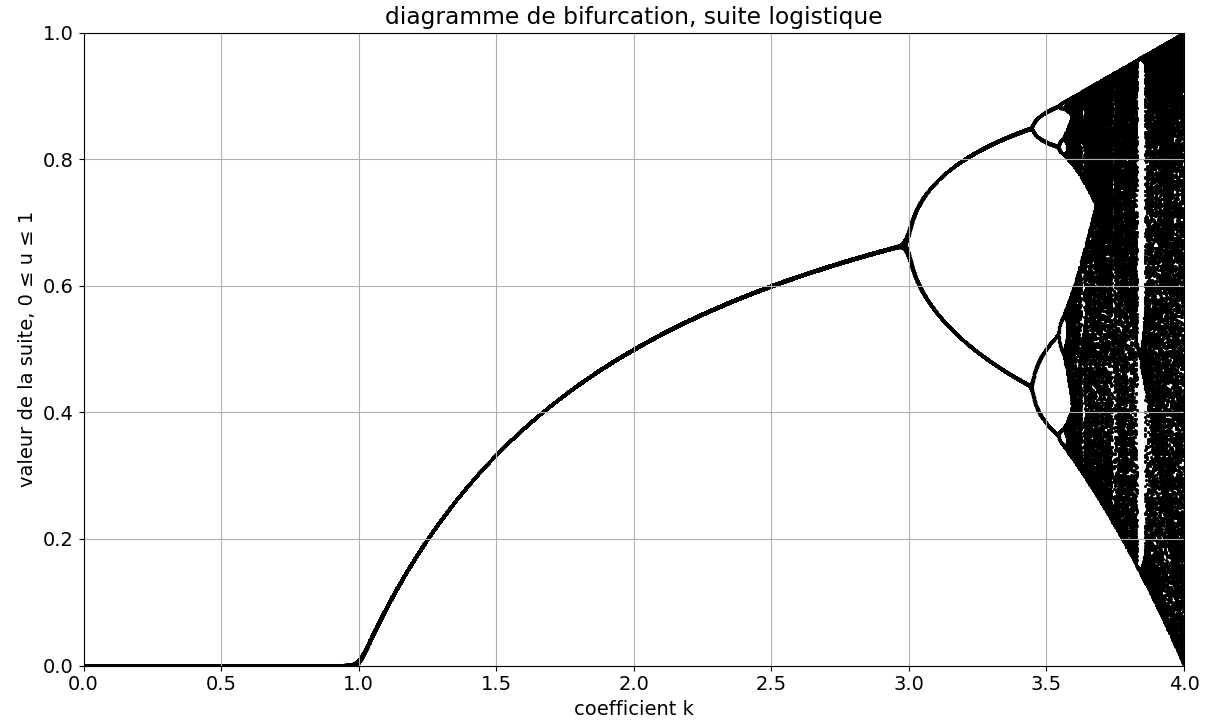
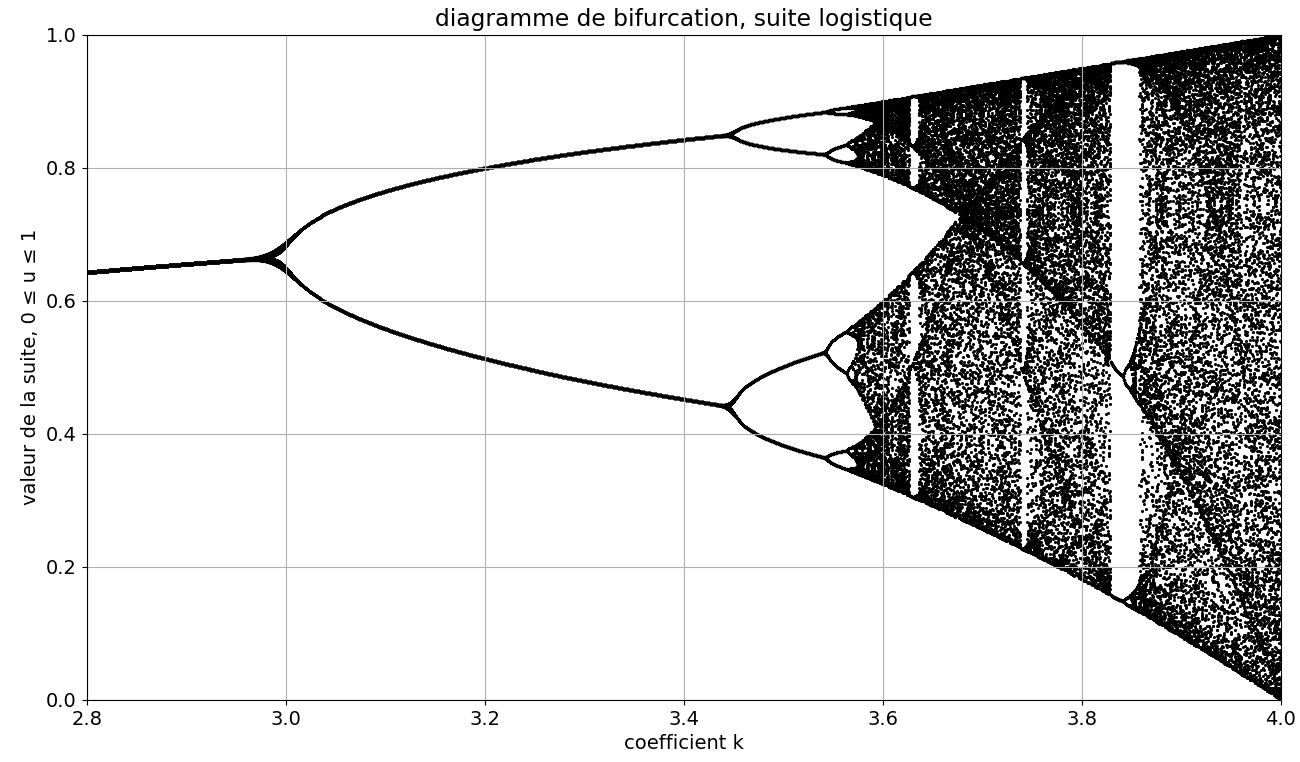
La figure 3 montre le diagramme de bifurcation pour des 0 ≤ k ≤ 4, la figure 4 est un zoom de la figure 3, pour les valeurs 2.8 ≤ k ≤ 4. Le chaos apparaît pour des valeurs de k supérieures à 3.6 environ.
Figure 3. Diagramme de bifurcation, suite logistique, pour 4000 valeurs de k entre 0 et 4 et pour 100 itérations par valeur, comprises entre la 100ème et la 199ème itération.. Entre k = 1.0 et k = 3.0 la suite converge vers une valeur limite unique. Puis elle converge vers deux valeurs, puis quatre, etc. Code pour cette image: suite logistique bifurcation
Cliquer sur l’image pour l’agrandir
Figure 4. Diagramme de bifurcation, suite logistique, pour 1200 valeurs de k entre 2.8 et 4 et pour 100 itérations de la suite par valeur. Agrandissement de la figure 3.
Cliquer sur l’image pour l’agrandir
2). L’oscillateur de Van der Pol
L’oscillateur de Van der Pol est un composant des débuts de l’électronique (figure 5).
Figure 5. Oscillateur de Van der Pol alimentant une lampe triode. Le forçage ou l’entretien des oscillations électromagnétiques est réalisé par la source Es qui alimente le circuit RLC au centre de l’image. Ug est la tension aux bornes du condensateur C. Image : wikipédia.
La forme de l’équation que nous allons utiliser dans les diverses modélisations est :
Où ε est le coefficient d’amortissement, A l’amplitude du forçage et ω sa fréquence, avec la source assurant le forçage, Es = Asin(ωt). Le terme d’amortissement est non-linéaire et le forçage est sinusoïdal. x(t) correspond à la tension électrique Ug. C’est une équation à une dimension.
Cette équation peut décrire plus généralement un système présentant des oscillations harmoniques amorties et à la fois entretenues. Dans le cas d’un système mécanique par exemple, on pourrait imaginer une masse oscillant au bout d’un ressort dont les oscillations sont amorties par un milieu résistant tout en étant entretenues par un moteur exerçant une force sinusoïdale sur le ressort. x(t) décrirait alors l’horaire de la masse.
Des résultats de résolution de l’équation sont donnés dans les figures 6 et 7, en faisant varier les paramètres ε, A et ω, et les conditions initiales x(0) et x'(0).
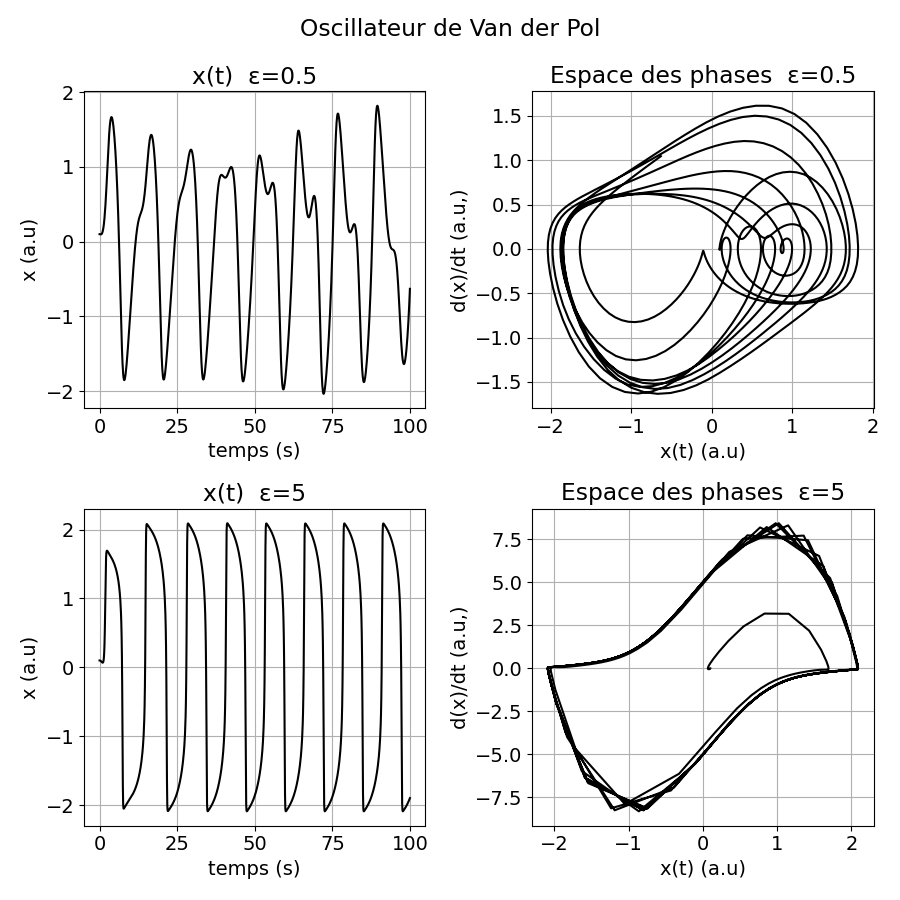
Figure 6. Oscillateur de Van der Pol. A droite la grandeur x est représentée en fonction du temps, à gauche on a représenté l’espace des phases correspondant. En haut, amortissement ε = 0.5 et en bas ε = 5. Les autres grandeurs sont A = 1, ω = 0.5 et pour les conditions initiales on a considéré et Pour ε = 0.5 on a un semblant de comportement chaotique. Code Python pour réaliser cette figure: chaos fig
Cliquer sur l’image pour l’agrandir
Figure 7. Oscillateur de Van der Pol. On a cherché les conditions pour avoir du chaos et sur wikipédia, il était proposé les valeurs A = 1.2, ω = 2π/10, ε = 8.53. Ensuite afin de tester la sensibilité aux conditions initiales, nous avons dessiné deux graphiques de x(t) pour les conditions initiales suivantes : x1(0) = 0 , x2(0) = 0.2 et x'(0) =0 , avec dans les deux cas. Le comportement chaotique semble assez évident. Code Python pour réaliser cette figure: chaos fig
Cliquer sur l’image pour l’agrandir
3). Le chaos de Lorenz
Edward Lorenz est le premier à avoir mis en évidence le chaos en météorologie dans les années 1960. Cherchant un modèle très simplifié des équations décrivant l’évolution de l’atmosphère, Lorenz s’est intéressé à modéliser le phénomène de convection de Rayleigh-Bénard. Les trois équations différentielles couplées obtenues sont les suivantes :
σ, ρ et β sont des paramètres positifs. σ est proportionnel à l’intensité du mouvement de convection, ρ est proportionnel à la différence de température entre les courants ascendants et descendants et β est proportionnel à l’écart du profil de température vertical par rapport à un profil linéaire.
Pour les valeurs des paramètres σ = 10, ρ = 28 et β = 8/3, le système dynamique différentiel de Lorenz présente un attracteur étrange, maintenant bien connu et largement popularisé sous le terme de « papillon » de Lorenz. Un attracteur étrange est une propriété des systèmes dynamiques chaotiques. Il représente une limite d’évolution des systèmes, quelles que soient les conditions initiales choisies.
Il est possible de représenter les solutions x, y et z dans un graphique à trois dimensions, comme sur la figure 8, où l’on a représenté le fameux papillon. On peut aussi choisir une des variables et la représenter en fonction du temps, en faisant varier les conditions initiales, comme sur la figure 9.
Figure 8. Solution des équations de Lorenz représentée dans un graphique x ,y, z à trois dimensions. Unités arbitraires.
Code Python pour réaliser cette figure: code fig Cliquer sur l’image pour l’agrandir
Figure 9. Représentation de la solution x(t) des équations de Lorenz, pour deux conditions initiales x(0) proches. Les deux solutions sont semblables jusqu’à t = 30 s, puis elles divergent clairement, indiquant un comportement chaotique. Code Python pour réaliser cette figure: code fig Petit extra: animation du dessin de cette figure, en Python ! lorentz x versus t avec chaos
Cliquer sur l’image pour l’agrandir
4). Le pendule double
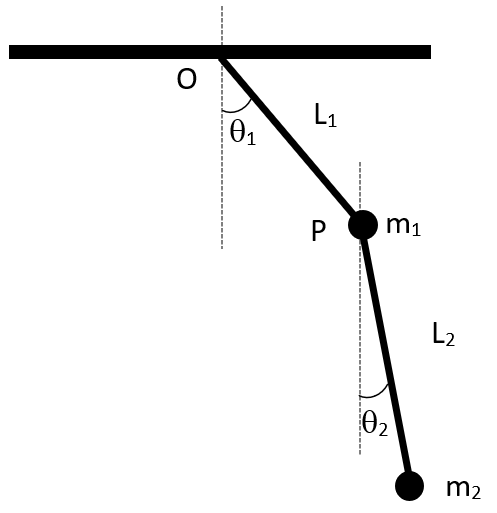
Facile d’accès par l’expérience, le pendule double représente l’exemple classique de mouvement chaotique avec sensibilité aux conditions initiales. La figure 10 schématise le pendule et indique les paramètres intervenant dans les équations du mouvement.
Figure 10. Pendule double. Le segment supérieur de longueur L1 est attaché en O et libre d’osciller dans une direction droite-gauche. La masse m1 est fixée à son extrémité. Le segment inférieur de longueur L2 s’articule en P, une masse m2 est fixée à son extrémité inférieure. Le pendule oscille dans le plan vertical de la feuille. A un instant t quelconque, Les segments L1 et L2 font les angles θ1 et θ2 respectivement avec la verticale. Les segments sont supposés de masses négligeables.
Les équations du mouvement sont retrouvées en appliquant la conservation de l’énergie. On obtient deux équations différentielles couplées, non linéaires pour les accélérations angulaires θ”1 et θ”2 . Le problème peut être simplifié en considérant que L1 = L2 = L et m1 = m2 = m. Cela donne :
L’équation (1) doit être encore insérée dans (2) afin d’exprimer θ”1 indépendamment de θ”2.
Même si ce système paraît horrible, sa résolution numérique ne pose aucun problème. On trouve alors les déplacements et vitesses angulaires en fonction du temps.
Les figures suivantes montrent certains résultats obtenus.
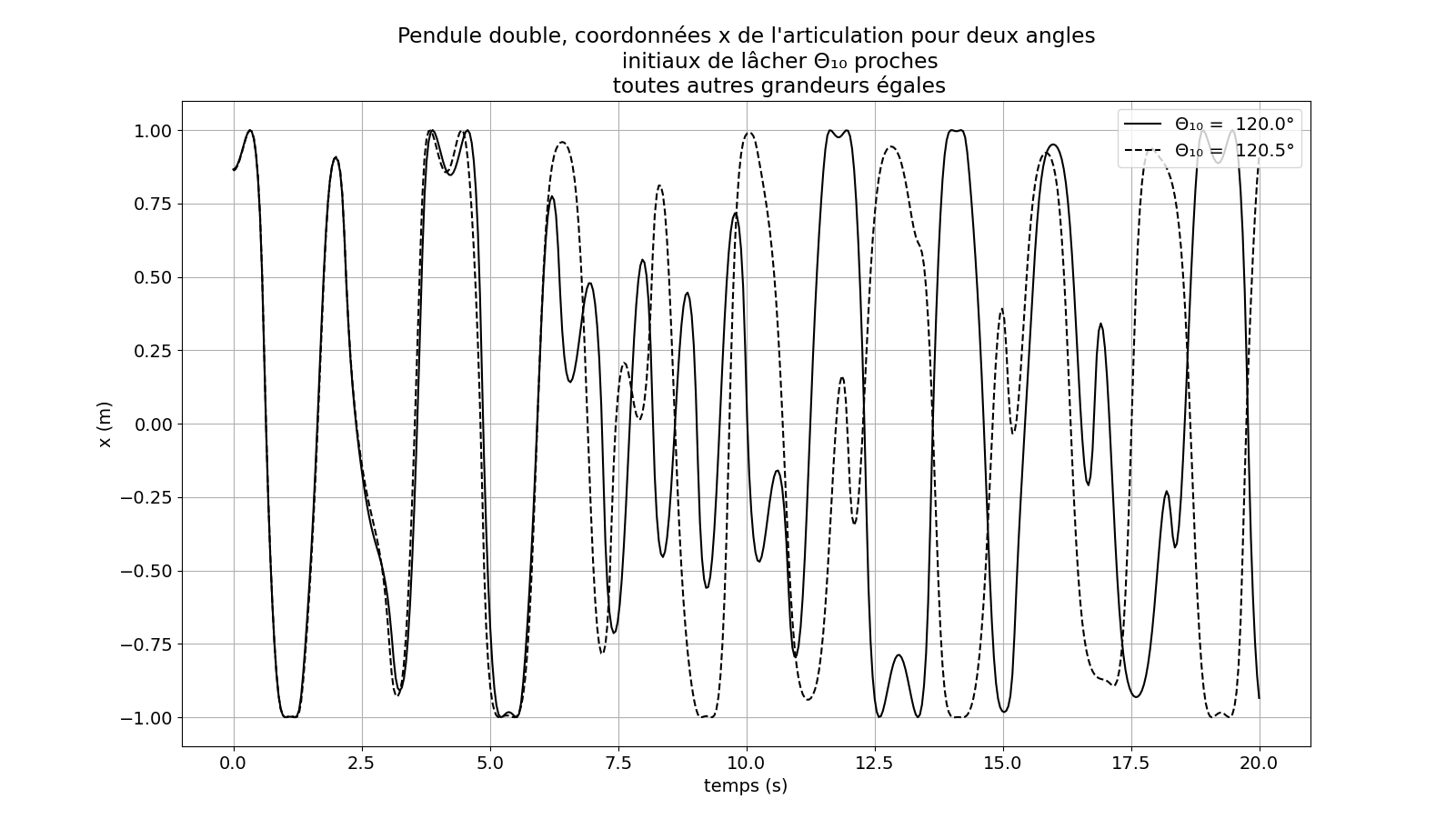
Figure 11. Pendule double, évolution de la coordonnées x du point P (articulation entre les deux pendules), pour deux angles de lâcher θ1 initiaux légèrement différents. Dans les deux cas, l’angle de lâcher initial θ2 a été fixé à –10°. Les vitesses angulaires initiales ont été fixées à 0. Voir la figure 10 pour le schéma du montage. Le comportement chaotique est clairement mis en évidence : après environ 2 secondes, les trajectoires s’écartent de plus en plus. Code Python pour réaliser cette figure: code fig
Cliquer sur l’image pour l’agrandir
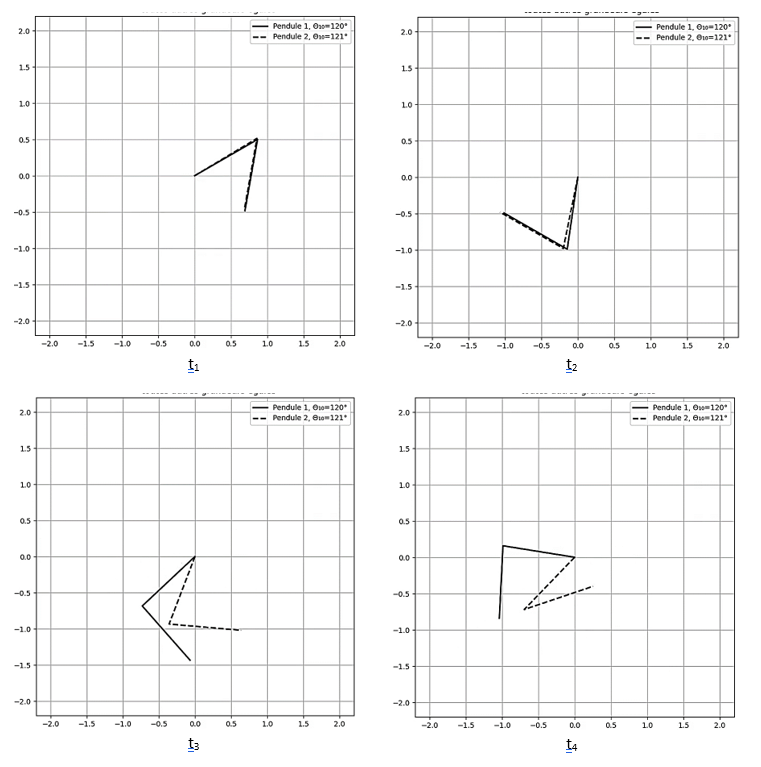
Figure 12. Captures d’écran d’une animation avec deux pendules double, prises à quatre instants différents, avec des temps t de prise de vue t1 < t2 < t3 < t4. Le lâcher a lieu sur l’image en haut à gauche. Un des pendules est en trait plein, l’autre en traitillés. Notez la structure du pendule avec ses deux segments articulés. La différence est de 1° entre les deux angles de lâcher θ1 , soit 120° et 121°. Dans les deux cas, l’angle de lâcher initial θ2 a été fixé à –10° comme on peut le soupçonner sur la première image. Les vitesses angulaires initiales ont été fixées à 0. Voir la figure 10 pour le schéma du montage. Le comportement chaotique est clairement mis en évidence.
Animation du mouvement du pendule double (vidéo de 10”): double_pendule_double
code Python de cette animation: double pendule animation code