Marche au hasard

 

La marche au hasard ou marche aléatoire (random walk en anglais) est une intéressante expérience de mathématiques appliquées. Elle trouve son origine en physique dans le problème du mouvement brownien, qui a permis de mettre en évidence l’existence des atomes et des molécules et de leur agitation thermique. Dans le mouvement brownien, de fines poussières en suspension dans l’air ou à la surface de liquides ont un mouvement aléatoire résultant des innombrables chocs avec les atomes ou molécules de leur environnement. Ces mouvements, repérés par R. Brown en 1827, ont été pour la première fois décrits mathématiquement par A. Einstein.

Ce problème se prête particulièrement bien à la modélisation informatique. Un dessin à la main des trajectoires peut être utile à faire tout au début de l’étude pour mieux se rendre compte de ce qui se passe.

 

1). La marche au hasard à une dimension

Imaginons une particule contrainte de se déplacer le long d’une droite horizontale, l’axe des x par exemple (ce choix est totalement libre). Notons positivement les déplacements de la particule vers la droite, négativement vers la gauche. Nous choisissons de faire partir la particule de l’origine x = 0. Durant un intervalle de temps Δt, la particule a le droit de se déplacer soit vers la droite d’une certaine quantité +d ou soit vers la gauche de la quantité -d. La probabilité de se déplacer vers la gauche est identique à la probabilité de se déplacer vers la droite, c’est-à-dire 1/2. Au bout d’un temps t = N×Δt, N entier, la particule se trouve en une position quelconque le long de l’axe.

Les positions successives de la particule peuvent être visualisées dans un graphique de l’horaire de la trajectoire.

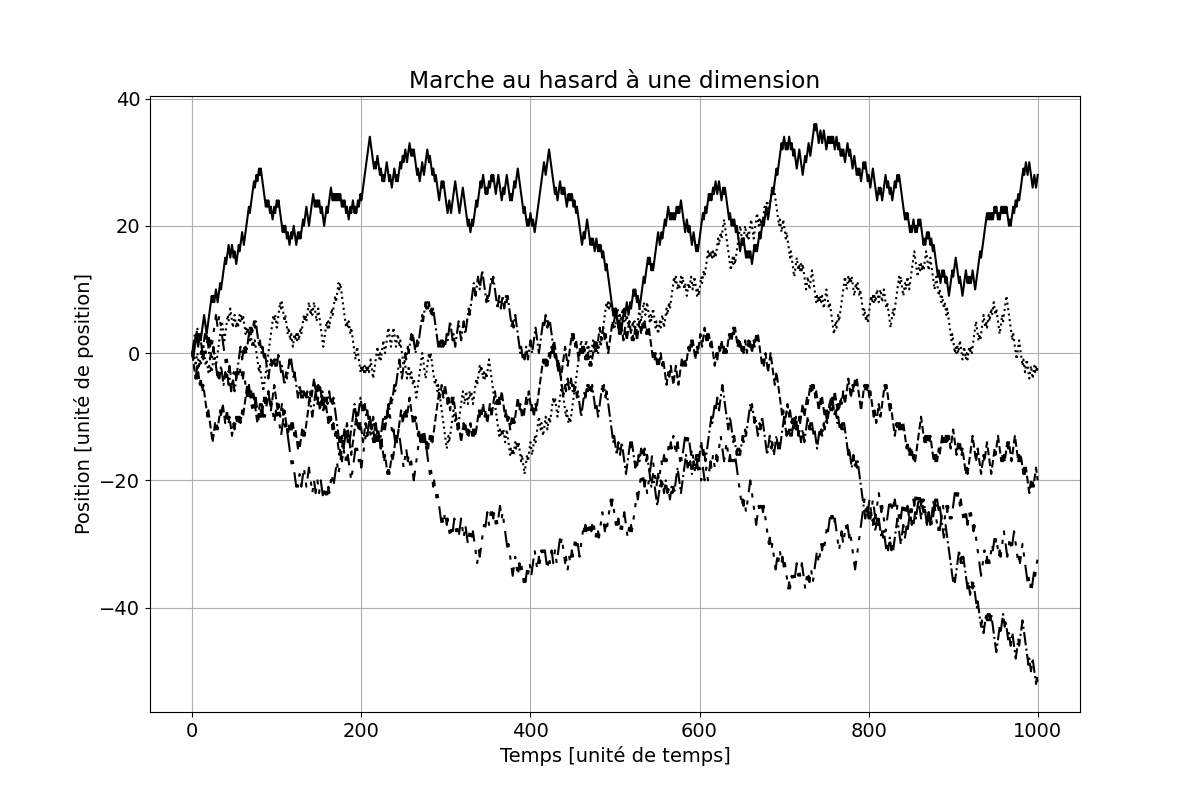
La figure 1 montre cinq de ces trajectoires aléatoires, pour des déplacements élémentaires de ± 1 et une unité de temps Δt = 1. Les unités de temps et de distance sont arbitraires, les déplacements identiques pour des durées identiques font que la vitesse de la particule est constante. La particule n’est jamais au repos : soit elle avance, soit elle recule.

Figure 1. Marche au hasard à une dimension, position en fonction du temps de parcours, pour N = 1000 unités de temps.

code pour dessiner la figure code fig 1

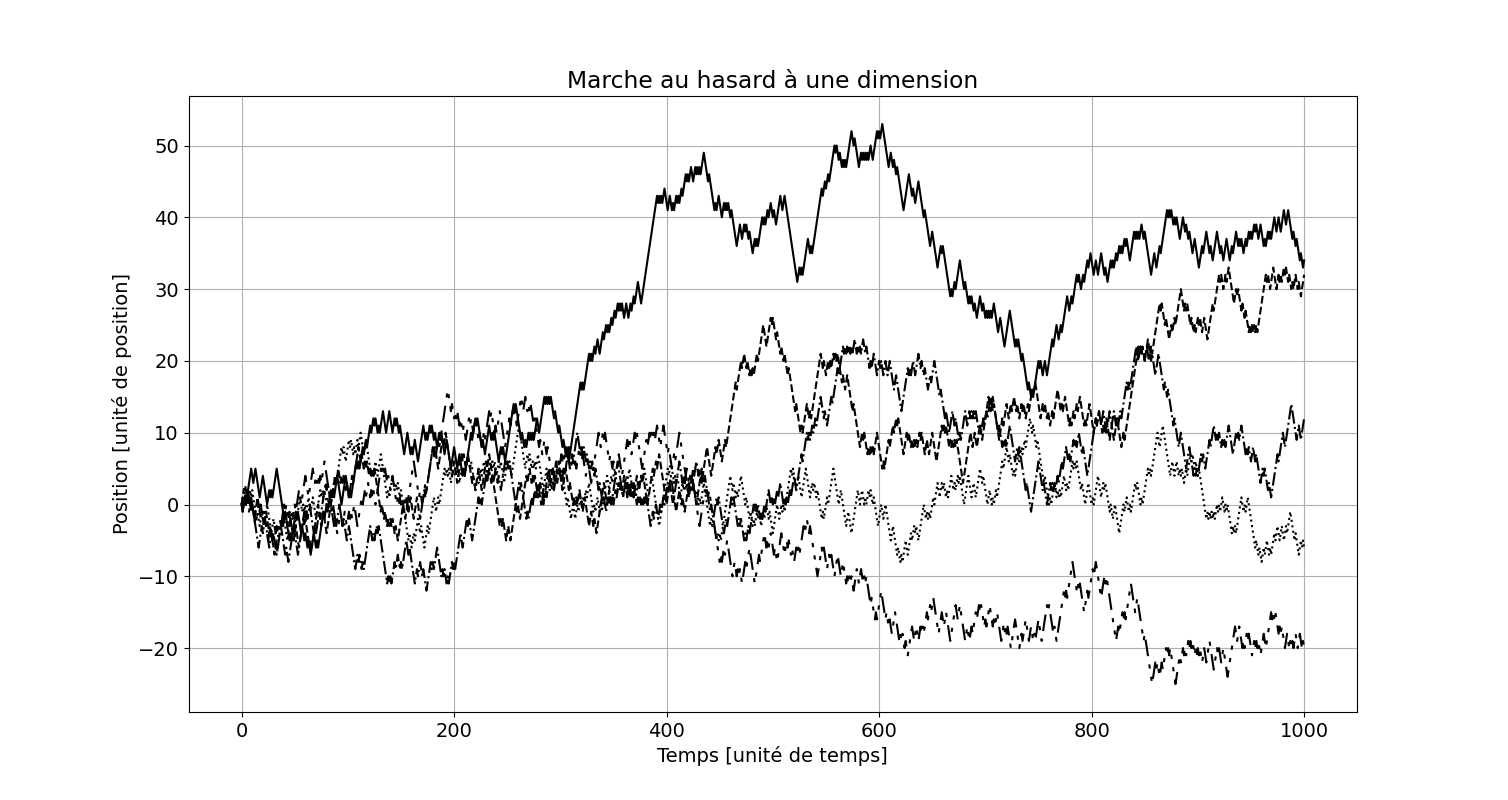
On voit que les trajectoires s’éloignent petit à petit de l’origine, mais cela est aléatoire. A l’extrême au bout du temps t = 1000, la particule pourrait se trouver en + 1000 ou en – 1000, mais cela est très peu probable ! 2 chances sur 2¹⁰⁰⁰ ! Une autre série de cinq trajectoires (figure 2) donne un résultat très différent, soulignant le caractère aléatoire du cheminement.

Figure 2. Même conditions que la figure 1, résultats différents.

 

Que se passe-t-il si l’on augmente encore la durée de la trajectoire ou la valeur de N ? Regardez la figure 3, pour un temps 10 fois plus grand !

Figure 3. Marche à une dimension, pour 10’000 unités de temps.

 

Les choses ne changent pas fondamentalement. Toutefois, il faut réaliser que l’on reste relativement proche de l’origine, car les positions possibles au bout d’un temps t = 10’000 varient de +10’000 à -10’000, alors que les trajectoires représentées ne sont pas plus éloignées que ± 100 à la fin des expériences.

 

2). La marche au hasard à deux dimensions

A deux dimensions on modélise des situations que l’on retrouve dans la réalité pour des petites particules flottant à la surface de liquides et ballotées dans toutes les directions par les mouvements sous-jacents, innombrables et invisibles des atomes et molécules du milieu. Il s’agit là du mouvement brownien classique, décrit par le botaniste R. Brown en 1827 et par la suite traité quantitativement par A. Einstein en 1905.

La particule part de l’origine et elle a le choix de se déplacer d’une unité, soit selon x (à gauche ou droite), soit selon y (en haut ou en bas). Chaque choix de mouvement est rigoureusement équiprobable, soit ¼. C’est le premier incrément. Ensuite, à partir de sa nouvelle position, la particule recommence son choix de direction, x ou y, droite-gauche, bas-haut et ainsi de suite. Les choix sont faits au hasard par l’ordinateur, il y a un algorithme intégré à Python qui s’en occupe. Est-ce du vrai hasard ? presque ! C’est en réalité très difficile d’avoir du vrai hasard, mais c’est une autre question…

Notons encore que la simulation se borne à considérer une vitesse partout constante de la particule, c’est-à-dire une unité de déplacement par incrément, ce qui n’est qu’une approximation de la réalité.

Le résultat montre le cheminement de la particule avec chaque changement de direction pouvant être interprétés comme une série de chocs particulièrement appuyés dans la direction suivie.

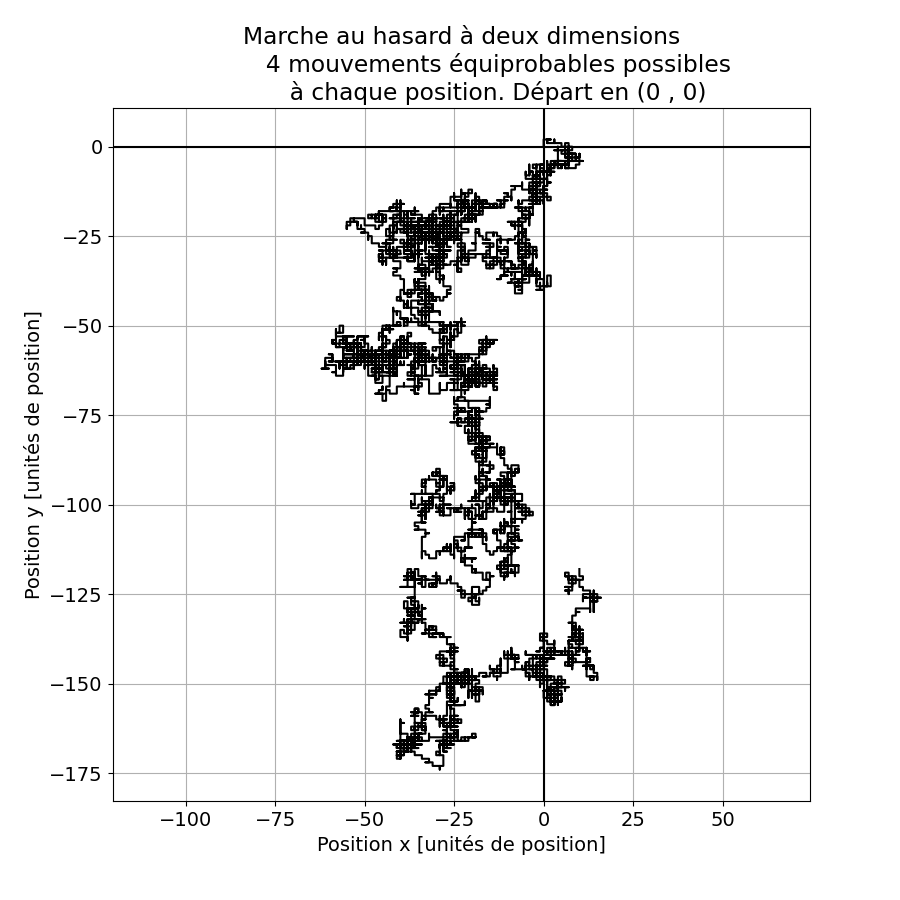
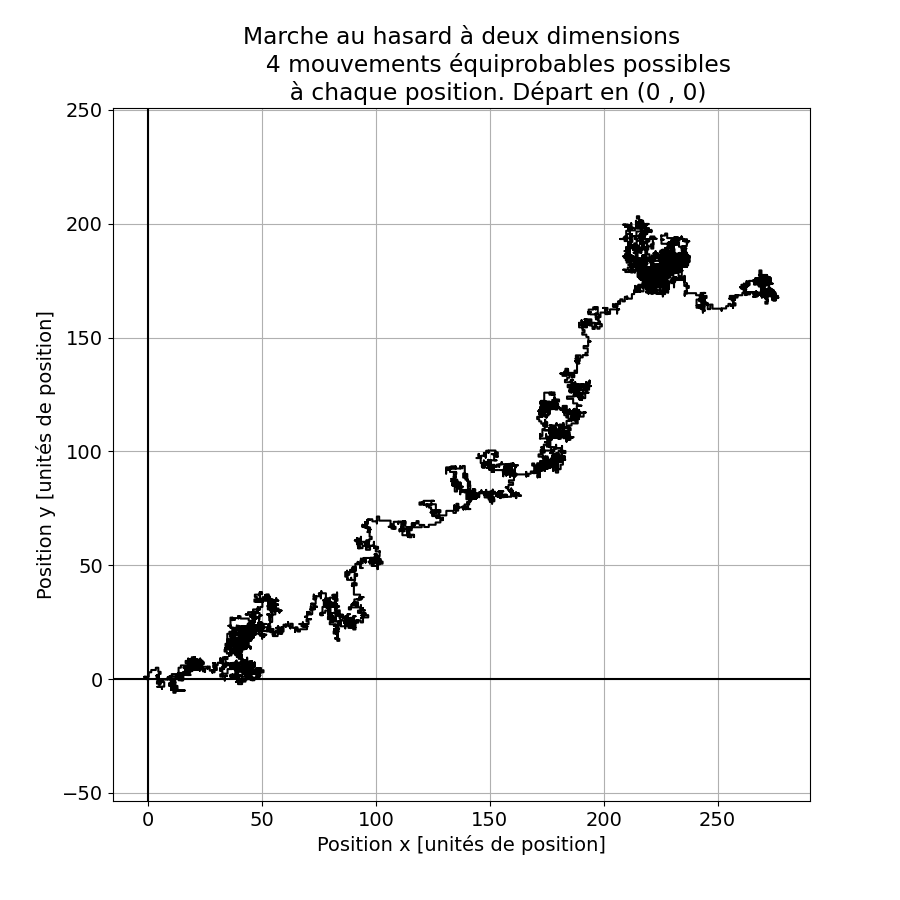
La figure 4 montre quatre résultats d’expériences numériques pour 10’000 déplacements élémentaires, de distance unité, de la particule.

 

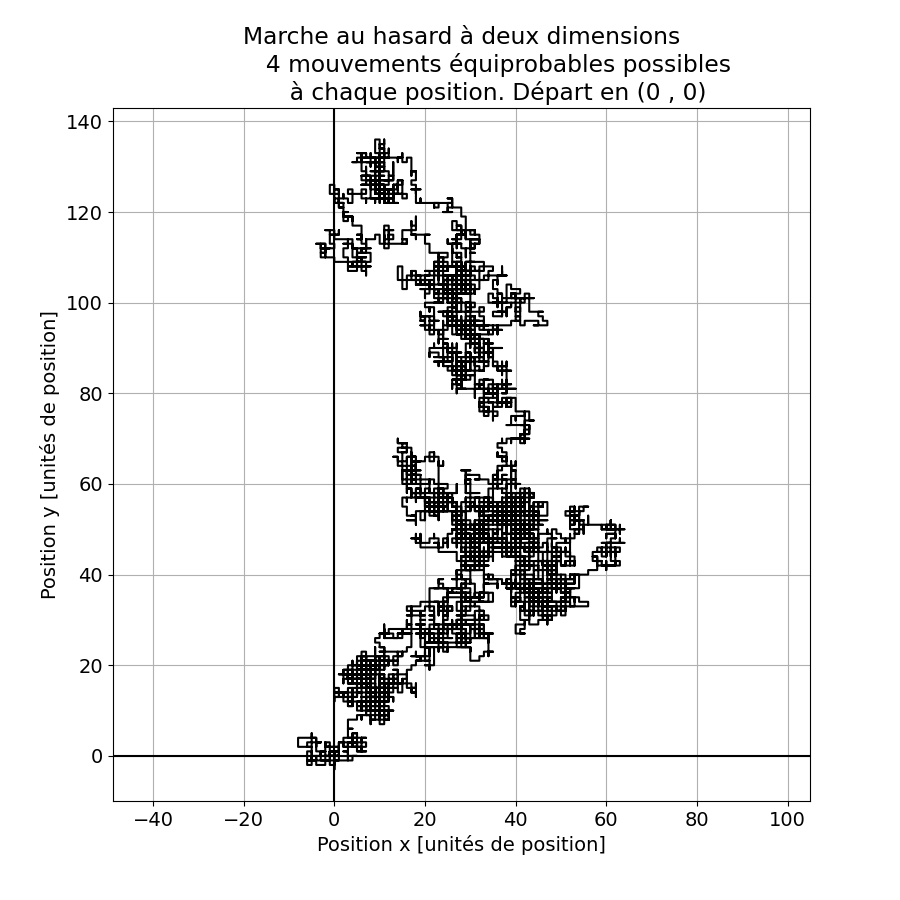
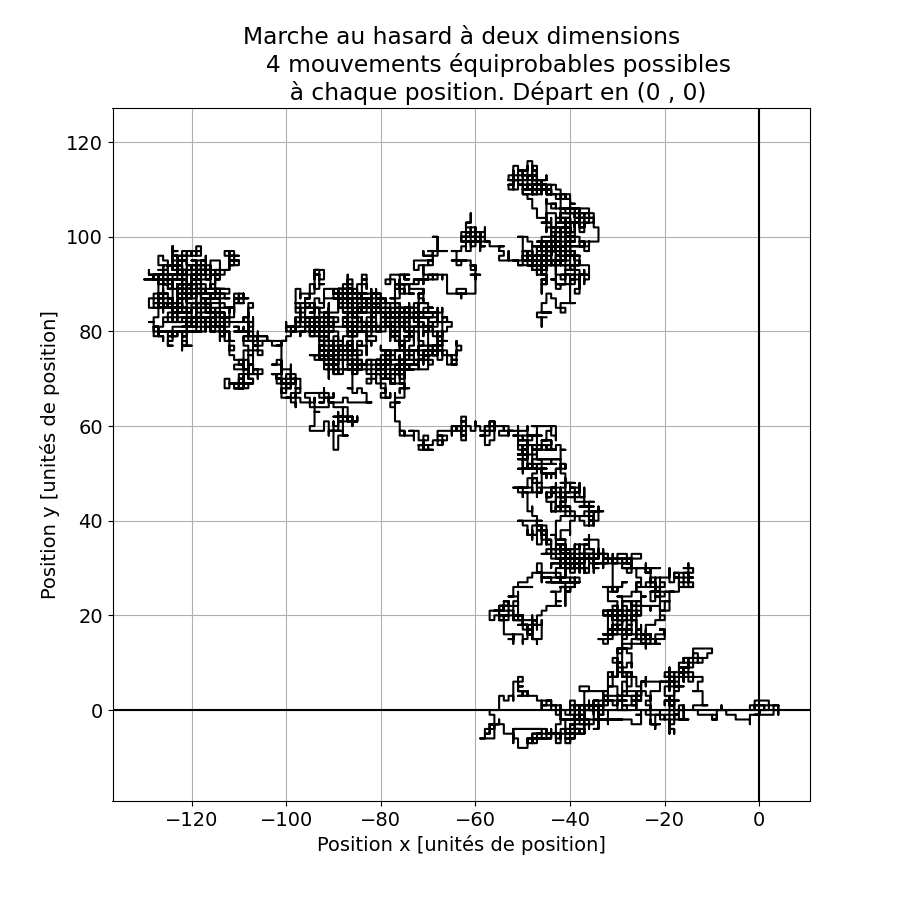Figure 4. La marche au hasard à deux dimensions représentées dans le plan classique (x, y). La particule part de l’origine et se déplace d’une unité à chaque fois, soit le long de x, soit le long de y, à choix. Un examen attentif des figures montre que les déplacements sont tous parallèles aux axes de coordonnées.  code: code fig 4

Ces résultats sont manifestement tous différents !

Comme en chaque position la particule a quatre possibilités de se déplacer (gauche-droite-haut-bas), avec 10’000 mouvements successifs, cela donne un nombre de 4^10’000 cheminement différents possibles !

Petite vidéo de la marche animée à deux dimensions (durée 30”): marche au hasard et son code: code marche animée

 

Il peut être aussi amusant d’aller plus loin est de considérer un mouvement d’ensemble du milieu sous-jacent qui fait qu’une direction de mouvement est privilégiée et que les longueurs des déplacements possibles ne sont plus identiques. Par exemple imaginons que les déplacements vers la droite (+x) et vers le haut (+y) valent 1, les déplacements vers la gauche (-x) et le bas (-y) valant -0.5, les choix demeurants équiprobables. C’est comme si le milieu sous-jacent coule dans la direction faisant un angle positif de 45° avec l’axe des x. Le résultat est donné par la figure 5.

Figure 5. Marche au hasard, mais avec des déplacements non identiques, privilégiant une direction donnée. Ici, on peut imaginer le fluide coulant vers le haut à droite.

 

C’est peut-être un peu exagéré ! alors choisissons plutôt des déplacements de 1 pour droite et haut et -0.9 pour gauche et bas. Le résultat est donné dans la figure 6.

Figure 6. Marche au hasard à deux dimensions, pour des déplacements environ 10% plus longs le long de +x et +y. Là le cheminement ressemble à des volutes de fumée de cigarette entraînées par un léger courant d’air !